Algorithm

스택 두 개로 큐 만들기 (Making Queue Using two Stacks)

  • 설계

    1. Stack 2개를 준비한다.
      • 하나는 inBox 스택, 다른 하나는 outBox 스택
    2. outBox가 비어있다면 inBox에 존재하는 값 전부를 outBox로 밀어 넣는다.
      • 이 때 inbox에 들어 있는 데이터의 순서가 LIFO에서 FIFO로 바뀐다.
    3. outBox에 있는 데이터를 pop 한다.

  • 구현

    import org.junit.jupiter.api.Test;
  
import java.util.Stack;
  
import static org.junit.jupiter.api.Assertions.assertEquals;
  
public class QueueTest {
    @Test
    public void test() {
        Queue<String> queue = new Queue<>();
        queue.enQueue("test1");
        queue.enQueue("test2");
        queue.enQueue("test3");
          
        assertEquals(queue.deQueue(), "test1");
        assertEquals(queue.deQueue(), "test2");
          
        queue.enQueue("test4");
          
        assertEquals(queue.deQueue(), "test3");
        assertEquals(queue.deQueue(), "test4");
    }
}
  
class Queue<T> {
      
    private Stack<T> inBox = new Stack();
    private Stack<T> outBox = new Stack();
      
    public void enQueue(T element) {
        inBox.push(element);
    }
      
    public T deQueue() {
        if (outBox.isEmpty()) {
            while (!inBox.isEmpty()) {
                outBox.push(inBox.pop());
            }
        }
          
        return outBox.pop();
    }
}

하노이 타워(Tower of Hanoi)

  • 설계

    • 출발지에 있는 n-1개의 원판을 경유지로 옮기는데 필요한 횟수 : M(n-1)
    • 출발지에 있는 한개의 원판을 도착지로 옮기는 필요한 횟수 : 1
    • 경유지에 있는 n-1개의 원판을 도착지로 옮기는데 필요한 횟수 : M(n-1)
    • 출발지에 있는 n개의 원판을 도착지로 옮기는데 필요한 횟수 : M(n) = 2M(n-1) + 1
    • M(n) = 2^n -1

  • 시간 복잡도

    • O(2^n)

  • 구현

    package com.webhook.receiver.slack.test;
  
import java.util.ArrayList;
  
public class TowerOfHanoi {
      
    ArrayList<int[]> seq;
      
    public int[][] solution(int n) {
        seq = new ArrayList<>();
          
        hanoi(n, 1, 3, 2);
          
        int[][] answer = new int[seq.size()][2];
        for(int i = 0 ; i < seq.size() ; ++i){
            int[] cmd = seq.get(i);
            answer[i][0] = cmd[0];
            answer[i][1] = cmd[1];
        }
          
        return answer;
    }
      
    private void hanoi(int n, int from, int to, int via){
        int[] move = {from, to};
          
        if(n == 1) {
            seq.add(move);
        } else {
            hanoi(n - 1, from, via, to);
            seq.add(move);
            hanoi(n - 1, via, to, from);
        }
    }
      
}

다익스트라(dijkstra) 알고리즘

  • 사용하는 이유
    • 그래프의 출발점에서 다른 점들로가는 최단거리를 구할 때 사용하는 알고리즘입니다.
  • 설계
    1. D[n] 배열을 만들고 모든 원소에 INFINITE 값을 넣어준다.
      • D[n] : 출발점 k로부터 각 정점까지의 최단 거리를 저장하는 배열
    2. 출발점(k)을 설정하고 D[k]에 0을 대입하고 k를 방문했다는 체크
    3. k에서 갈 수 있는 정점들의 최단 거리를 D[n]에 반영한 후 최단 거리를 가진 정점을 방문했다는 체크
    4. k에서 방문한(체크된) 점들을 통해 갈 수 있는 정점들의 최단 거리를 D[n]에 반영한 후 최단 거리를 가진 정점을 방문했다는 체크
    5. 모든 점이 방문될 때까지 4번 반복
  • 시간 복잡도
    • 인접 리스트
      • 인접 리스트는 각 정점마다 인접한 간선들을 모두 검사하는 작업(O(E))과 우선순위 큐에 원소를 모두 넣고 heapify하는 작업(O(logE))이 존재합니다. 이 두 작업을 수행하는데 걸리는 시간복잡도는 (O(ElogE))이지만 E는 V^2보다 작기 때문에 O(logE) = O(logV)라고 볼 수 있습니다. 따라서 시간 복잡도는 O(ElogV) 입니다.
        • (|E| <= |V|^2) == (log|E| <= 2log|V|) == (O(log|E|) == O(log|V|))
    • 인접 행렬
      • 배열에서는 모든 점을 탐색해야 하기 때문에 시간 복잡도는 O(V^2) 입니다.

빅오 표기법

두 개의 함수 f(n)과 g(n)이 주어졌을 때 모든 n >= n0 에 대하여 |f(n)| <= c|g(n)| 을 만족하는 2개의 상수 c와 n0가 존재하면 f(n) = O(g(n)) 이다.

정렬(Sorting) 알고리즘

  • 버블 정렬(Bubble Sort)

    • 서로 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환하는 알고리즘

    • 맨 끝에서부터 자료를 정렬하는 알고리즘이다.

    • 입력된 배열 이외에 추가적인 메모리가 필요하지 않다. (제자리 정렬)

    • 시간 복잡도(비교 횟수)

      • (n-1) + (n-2) + (n-3) + … + 2 + 1 = ((n-1) * n) / 2 = O(n^2)

    • 그림

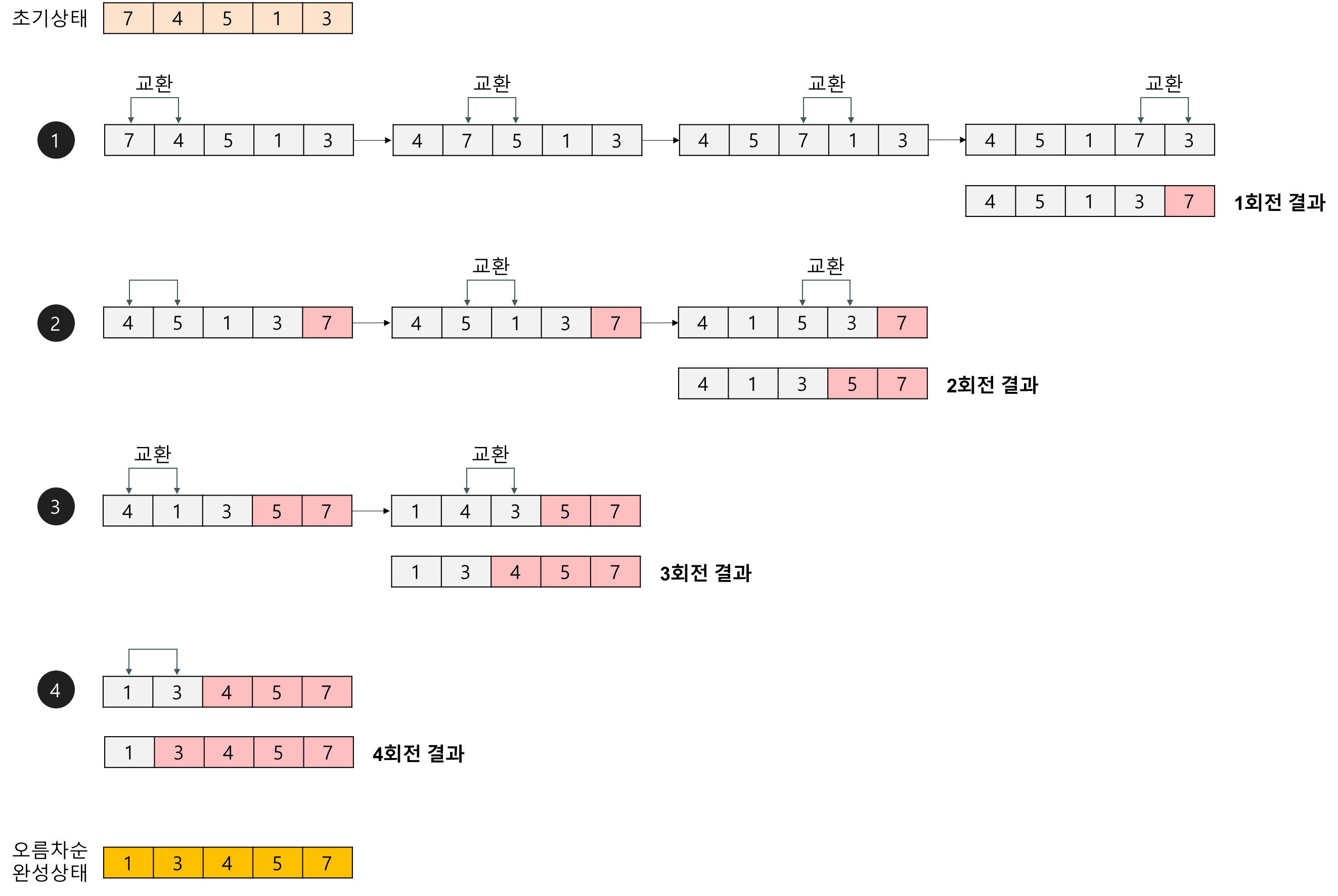
    • 구현

      public class BubbleSorting {
    @Test
    public void bubbleSortingTest() {
        int[] array = {3,1,2,5,6,9,2};
            
        for (int i = array.length -1 ; i > 0 ; i --) {
            for (int j = 0 ; j < i ; j ++) {
                if (array[j] > array[j+1]) {
                    int temp = array[j+1];
                    array[j+1] = array[j];
                    array[j] = temp;
                }
            }
        }
        
        Arrays.stream(array).forEach(i -> System.out.print(i + " "));
    }
}

  • 선택 정렬(Selection Sort)

    • 배열에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘

    • 보통 가장 처음이나 가장 마지막 위치부터 정렬하는 알고리즘이다.

    • 입력된 배열 이외에 추가적인 메모리가 필요하지 않다. (제자리 정렬)

    • 시간 복잡도(비교 횟수)

      • (n-1) + (n-2) + (n-3) + … + 2 + 1 = (n-1)n / 2 = O(n^2)

    • 그림

    • 구현

      public class SelectionSorting {
        
    @Test
    public void selectionSortingTest() {
        int[] array = {3,1,2,5,6,9,2};
        
        for (int i = 0; i < array.length; i++) {
            int minValueIndex = i;
            for (int j = i; j < array.length; j++) {
                if (array[minValueIndex] > array[j]) {
                    minValueIndex = j;
                }
            }
            int temp = array[minValueIndex];
            array[minValueIndex] = array[i];
            array[i] = temp;
        }
        
        Arrays.stream(array).forEach(i -> System.out.print(i + " "));
    }
}

  • 삽입 정렬(Insertion Sort)

    • 2번째 레코드부터 앞의 레코드들을 보며 자신이 위치해야 할 곳으로 삽입하면서 정렬하는 알고리즘

    • k번째 레코드는 1 ~ (k-1) 번째 레코드들과 비교해야 한다.

    • 보통 가장 처음이나 가장 마지막 위치부터 정렬하는 알고리즘이다.

    • 입력된 배열 이외에 추가적인 메모리가 필요하지 않다. (제자리 정렬)

    • 시간 복잡도(비교 횟수)

      • 1 + 2 + … + (n-3) + (n-2) + (n-1) = (n-1)n / 2 = O(n^2)

    • 그림

    • 구현

      public class InsertionSorting {
    @Test
    public void insertionSortingTest() {
        int[] array = {3, 1, 2, 5, 6, 9, 2};
            
        for (int i = 1; i < array.length; i++) {
            int temp = array[i];
            for (int j = i - 1; j >= 0; j--) {
                if (array[j] > temp) {
                    array[j + 1] = array[j];
                    array[j] = temp;
                } else {
                    break;
                }
            }
        }
            
        Arrays.stream(array).forEach(i -> System.out.print(i + " "));
    }
}

  • 합병 정렬(Merge Sort)

    • 하나의 리스트를 원소의 크기가 1이 될 때까지 분할한 후 분할된 리스트들을 합하여 전체가 정렬된 리스트가 되게 하는 알고리즘

    • 분할 정복(Divide and Conquer)을 사용하는 대표적인 정렬 방법

    • 합병 정렬을 Array로 구현한다면 추가적인 메모리가 필요하지만 LinkedList로 구현한다면 필요하지 않다.

    • 설계

      1. 분할(Divide) : 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
      2. 정복(Conquer) : 부분 배열을 정렬한다.
      3. 결합(Combine) : 정렬된 부분 배열들을 하나의 배열에 합병한다.

    • 그림

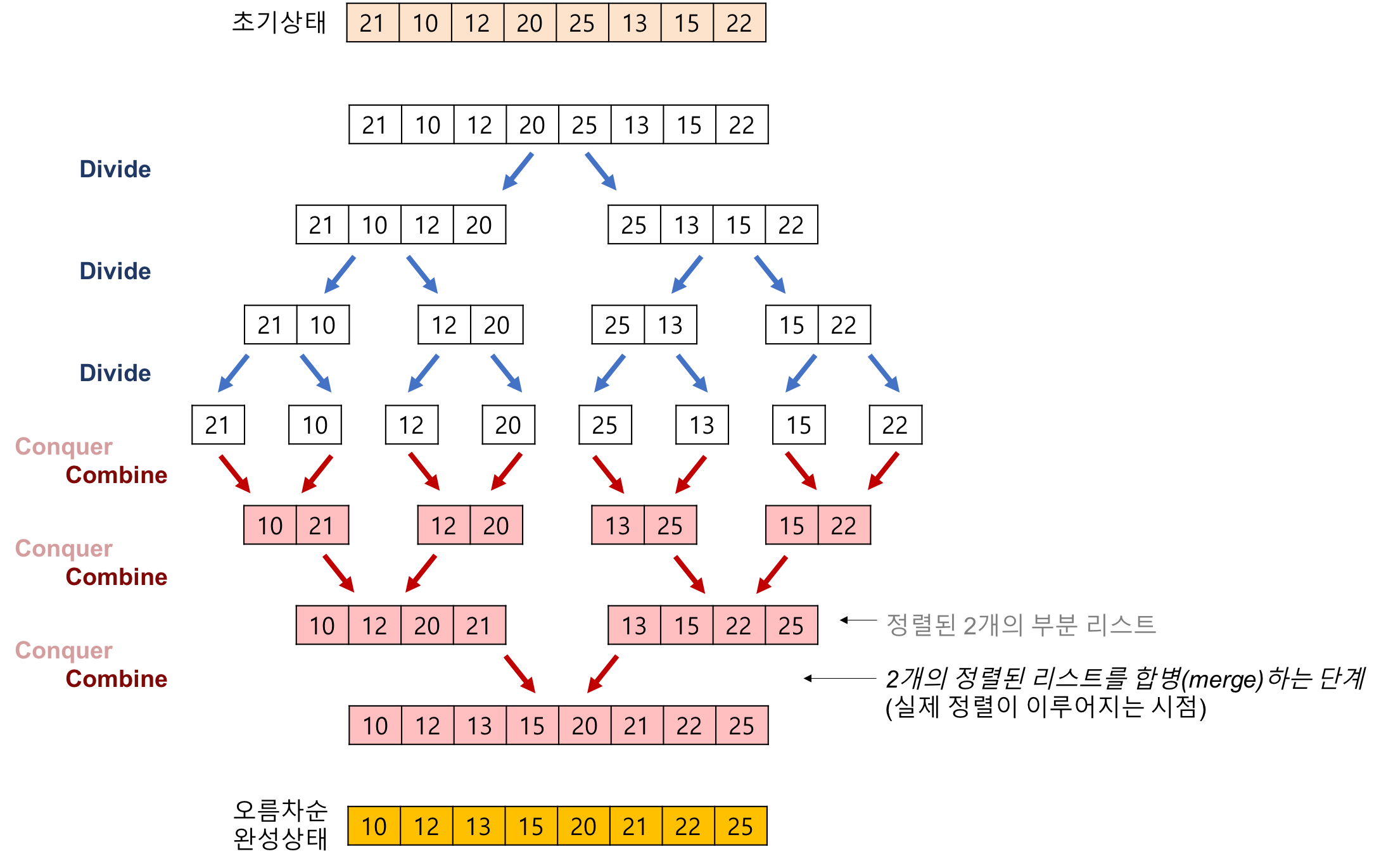
    • 시간 복잡도

      • 합병 단계의 비교 횟수는 nlogn 이고 이동 횟수는 2nlogn 이 발생하기 때문에 시간복잡도는 다음과 같다. T(n) = nlogn(비교) + 2nlogn(이동) = 3nlogn = O(nlogn)

  • 힙 정렬(Heap Sort)

    • 리스트의 원소들를 힙으로 구성해서 정렬하는 알고리즘 (max heap 또는 min heap 사용)
      • 배열로 힙을 구성할 경우 index를 1부터 시작하면 부모 노드와 자식 노드간의 인덱스를 계산하기 쉽다.
    • 힙 정렬은 시간복잡도가 좋은 편이고 전체 자료 정렬시 사용하기 보다는 상위의 큰 값 몇개만 필요할 때 사용하는게 가장 좋다.
    • 시간 복잡도(비교 횟수)
      • heapify 하는데 걸리는 시간이 O(logn)이기 때문에 n개를 정렬하는데 걸리는 시간 복잡도는 O(nlogn)이다.

  • 퀵 정렬(Quick Sort)

    • 리스트 안의 한 요소 즉, pivot을 고르고 pivot을 기준으로 작은 요소들은 왼쪽으로 보내고, 큰 요소들은 오른쪽으로 보냅니다. pivot을 제외한 왼쪽과 오른쪽 리스트 각각이 더 이상 분할이 불가능할 때까지 위 작업을 반복하며 분할이 끝난 후 병합을 통해서 정렬하는 알고리즘

    • 분할 정복(Divide and Conquer)을 사용하는 대표적인 정렬 방법

    • Merge Sort와 달리 퀵 정렬은 리스트를 비균등하게 분할한다.

    • 설계

      • 분할(Divide) : 입력 배열을 pivot을 기준으로 비균등하게 2개의 부분 배열(pivot을 중심으로 왼쪽 배열은 피벗보다 작은 요소들이 존재하고 오른쪽 배열은 피벗보다 큰 요소들이 존재)로 분할한다.
      • 정복(Conquer) : 부분 배열을 정렬한다.
      • 결합(Combine) : 정렬된 부분 배열들을 하나의 배열로 병합한다.

    • 그림

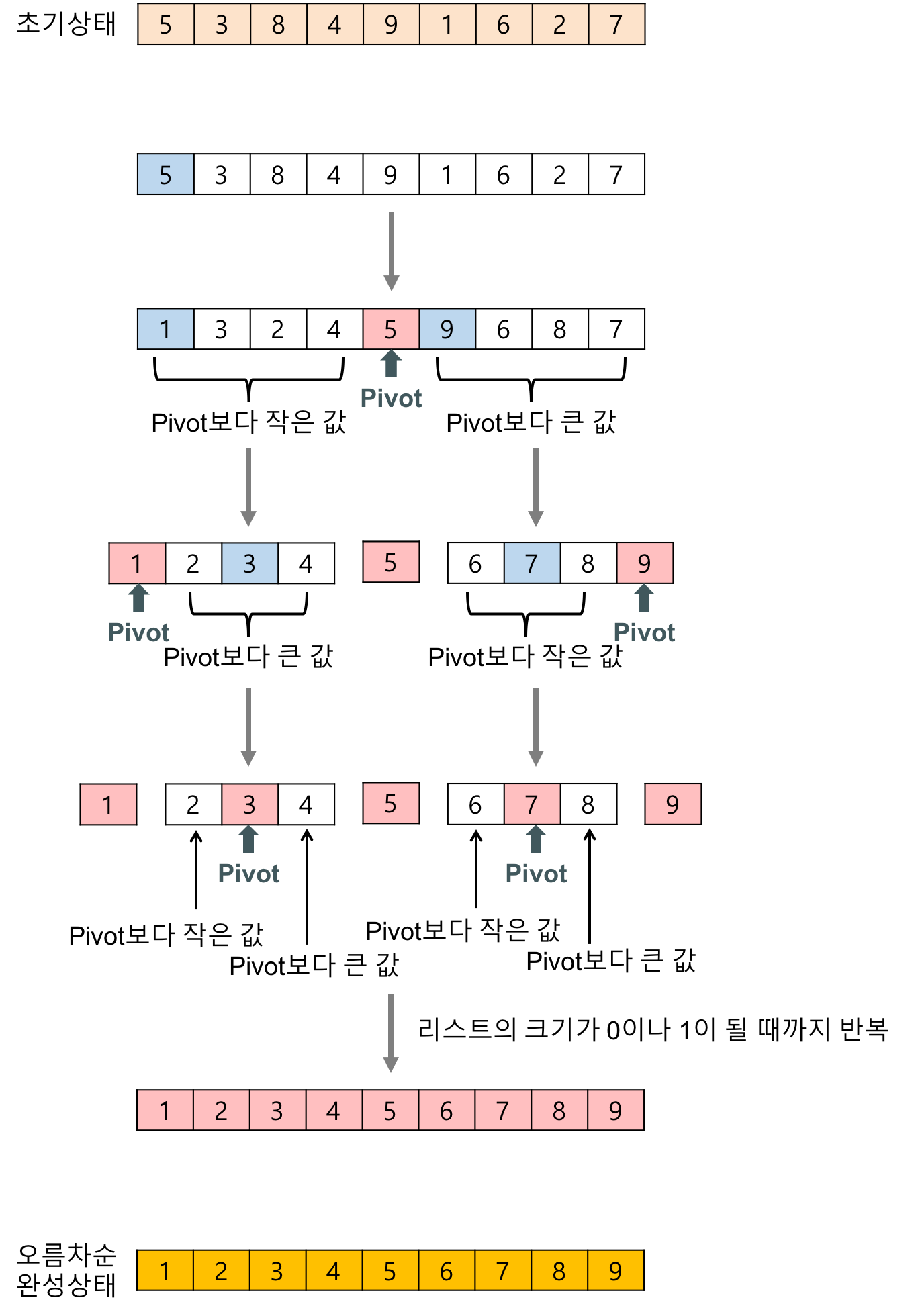
    • 시간 복잡도

      • 최악의 경우 시간 복잡도는 O(n^2)
        • 비 균등 분할이기 때문에 최악의 경우 순환 호출의 깊이가 n이 될 수 있고 각 순환 호출 단계에서 평균 n번 정도의 비교가 이루어지기 때문에 최악의 경우 시간 복잡도는 O(n^2)이다.
      • 평균 시간 복잡도는 O(nlogn)이다.
        • 평균의 경우 높이가 logn 이고 각 순환 호출 단계에서 평균적으로 n번의 비교가 이루어 지기 때문에 평균의 경우 시간 복잡도는 O(nlogn)이다.

    • 최악의 경우 시간복잡도가 O(n^2) 이지만 시간 복잡도가 O(nlogn)인 힙 정렬, 병합 정렬보다 보통 빠르다.

Github Pages

어떤 블로그를 운영중이시며 왜 운영하시나요?

개발자로서 성장하는 과정과 지식을 학습하고 적용하면서 발생한 이슈, 문제를 해결한 경험 등을 공유하기 위한 블로그를 Github Pages 에서 운영하고 있습니다. 여러 개발자들이 작성한 블로그를 통해서 제가 도움을 받았던 것 처럼 저 또한 많은 개발자분들에게 도움을 드리고 싶어서 블로그를 운영하게 되었습니다. 또한 다른 사람에게 경험과 지식을 공유하면서 제 지식의 깊이도 늘릴 수 있는 기회를 만들고자 블로그를 운영하게 되었습니다.

Github Pages란 무엇인가요?

Github Pages란 Github 저장소의 내용을 웹사이트로 만들어주는 정적 웹 사이트 호스팅 서비스(Static Website Hosting Service)를 의미합니다.

다양한 블로깅 플랫폼이 존재하는데 왜 Github Pages를 사용했나요?

Tistory나, Velog, Medium 등의 대부분의 블로깅 플랫폼은 아주 다양한 테마와 편리한 기능들을 지원해 줍니다. 이러한 기능들을 사용해서 나만의 멋진 블로그를 만들 수 있었지만 모든 기능과 테마가 플랫폼에 종속되어 있기 때문에 나만의 특징을 가진 블로그를 만들기에는 한계가 존재했습니다. 이를 해결하고자 좀 더 로우 레벨인 정적 웹 사이트 호스팅 서비스인 Github Pages를 사용해 나만의 특징을 가진 블로그를 만들었습니다.

어떤 정적 사이트 생성기를 활용하여 Github Pages를 사용하셨나요?

저는 Jekyll이라고 하는 Ruby 기반의 정적 사이트 생성기를 사용해서 블로그를 운영하고 있습니다.

Ruby

루비(Ruby)는 동적 객체 지향 스크립트 프로그래밍 언어이다. 루비는 순수 객체 지향 언어라, 정수나 문자열 등을 포함한 데이터 형식 등 모든 것이 객체이다.

Ruby의 기능에는 클래스 정의, 가비지 컬렉션, 강력한 정규 표현식 처리, 다중 스레드, 예외 처리, 반복, 클로저, Mixin, 연산자 오버로드 등이 있다. 구문은 ALGOL계를 계승하면서 가독성을 중시하고 있다.

왜 Jekyll을 사용했는가?

Jekyll을 사용한 이유는 Github Pages가 Jekyll을 기본 엔진으로 사용하고 있고 마음에 드는 템플릿이 대부분 Jekyll을 사용해서 만들어졌기 때문에 사용했습니다.

Jekyll을 사용하는데 어려움이 없었는가??

Jekyll을 사용하는데 어려움으로는 처음 블로깅 환경을 구성하는데 어려움이 있었습니다. 정적 사이트 생성기라서 단순할 줄 알았지만 생각보다 복잡했고 어떤 모듈이 어떠한 역할을 하는지에 대해 파악하는데 어려웠습니다.

어떻게 어려움을 극복하게 되었는가??

제가 사용하는 Jekyll 템플릿을 만든 개발자가 확장성 및 유지보수성 있는 코드 작성과 모듈화를 해주어서 처음 블로깅 환경을 구성하는데 많은 도움이 되었습니다. 그래도 모르는 부분은 직접 모듈 하나 하나를 뜯어보거나 공식 문서를 통해서 이슈를 해결했던 것 같습니다.

구체적으로 어려움이 무엇이었는가??

제가 원하는 디자인의 블로그를 만들면서 이슈가 발생했습니다. 블로그의 메인 컬러라는 property가 존재했고, 이는 블로그의 메인 컬러 뿐만 아니라 텍스트의 색깔에도 종속되어 있었습니다. 이를 해결하기 위해 저는 properties파일에서 메인 컬러 Property를 배경 Color와 텍스트 색깔 property를 나누었고 관련 코드를 바꿈으로써 제가 원하는 디자인을 가진 블로그를 만들 수 있었습니다.